Deriving Bernoullis equation

To derive Bernoulli’s equation, we apply the work–energy theorem to the fluid in a section of a flow tube. In Fig. 12.23 we consider the element of fluid that at some initial time lies between the two cross sections a and c. The speeds at the lower and upper ends are v1 and v2. In a small time interval dt, the fluid that is initially at a moves to b, a distance ds₁ = v₁ dt, and the fluid that is initially at c moves to d, a distance ds₂ = v₂ dt. The cross-sectional areas at the two ends are A₁ and A₂, as shown. The fluid is incompressible; hence by the continuity equation, Eq. (12.10), the volume of fluid dV passing any cross section during time dt is the same. That is, dV = A₁ ds₁ = A₂ ds₂.

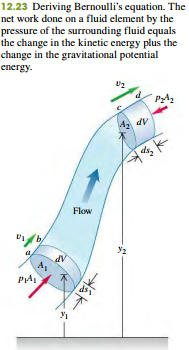
Let’s compute the work done on this fluid element during dt. If there is negligible internal friction in the fluid (i.e., no viscosity), the only nongravitational forces that do work on the element are due to the pressure of the surrounding fluid. The pressures at the two ends are p₁ and p_2; the force on the cross section at a is p₁A₁, and the force at c is p₂A₂. The net work dW done on the element by the surrounding fluid during this displacement is therefore

The term p₂A₂ds₂ has a negative sign because the force at c opposes the displacement of the fluid.

The work dW is due to forces other than the conservative force of gravity, so it equals the change in the total mechanical energy (kinetic energy plus gravitational potential energy) associated with the fluid element. The mechanical energy for the fluid between sections b and c does not change. At the beginning of dt the fluid between a and b has volume A1 ds1, mass rA1 ds1, and kinetic energy 1/ 2 r(A₁ ds₁2v₁ ). At the end of dt the fluid between c and d has kinetic energy 1/ 2 r₁A₂ ds₂v₂ ². The net change in kinetic energy dK during time dt is

What about the change in gravitational potential energy? At the beginning
of time interval dt, the potential energy for the mass between a and b is
dm gy1 = r dV gy1. At the end of dt, the potential energy for the mass between c
and d is dm gy2 = r dV gy_2. The net change in potential energy dU during dt is

Combining Eqs. (12.13), (12.14), and (12.15) in the energy equation dW = dK + dU, we obtain

This is Bernoulli’s equation. It states that the work done on a unit volume of fluid by the surrounding fluid is equal to the sum of the changes in kinetic and potential energies per unit volume that occur during the flow. We may also interpret Eq. (12.16) in terms of pressures. The first term on the right is the pressure difference associated with the change of speed of the fluid. The second term on the right is the additional pressure difference caused by the weight of the fluid and the difference in elevation of the two ends

We can also express Eq. (12.16) in a more convenient form as

Subscripts 1 and 2 refer to any two points along the flow tube, so we can write

Note that when the fluid is not moving (so v1 = v2 = 0), Eq. (12.17) reduces to
the pressure relationship we derived for a fluid at rest, Eq. (12.5).

Caution bernoulli’s equation applies in certain situations only We stress again that
Bernoulli’s equation is valid for only incompressible, steady flow of a fluid with no internal
friction (no viscosity). It’s a simple equation, but don’t be tempted to use it in situations
Demo in which it doesn’t apply! 

Frequently Asked Questions